Extension
Estimating the Size of a Population
One of the basic questions in ecology is how many animals are there in a population?
This is not a question that can be answered easily – without somehow catching them all and counting them!
There is a way, however, where we can ‘estimate’ the number of animals in a population, with a certain margin of error. To do this we need to somehow mark a certain number of the animals in such a way that we can recognise them. For example, by tagging them, or placing a visible paint mark on them.
The ‘dilution principle’
We use a process called ‘the dilution principle’ to estimate the size of the population.
It was first used in the field of health, to measure the concentration required of a therapeutic substance in the blood.
For the therapeutic substance to be effective at its site of action, the total blood volume of the patient needs to be calculated.
Next, how much of the substance needs to be added for it to arrive at its site of action at the correct concentration.
METHOD
1. Inject a known amount of marker substance, for example 5g (which we call X).
2. After sufficient time for the dye to equilibrate throughout the circulation, a blood sample is taken and the concentration of dye is measured, for example 0.1g/ml (which we call Y).
3. The total volume of blood can then be calculated as the dilution of X, as X/Y, or 5/0.1 = 50ml.
Activity
An Ant Colony:
• The dilution principle assumes that the sample of marked animals is thoroughly mixed with the unmarked animals when returned to the population.
• Later, we take a sample, count them, and record how many of them are marked.
• The proportion of those marked animals in the sample is equivalent to the proportion of the number of animals marked in the whole population.
We tried this exercise with the large’ Sergeant’ or ‘Bull’ ant that belong to the genus of ancient ants known as Myrmecia. If you find an ant’s nest with active ants coming and going, this might work for you. Watch the video clip Marking ants.MOV (TOOLBOX).
EQUIPMENT
Bottle Bic White-Out, with applicator
METHOD
These are aggressive ants with a nasty bite so do not handle them in any way.
1. As each ant moved from the nest, we quickly dabbed a spot of white paint on the rear of the abdomen, using the small paint brush from Bic White-Out. This dries rapidly and does not harm the ant.
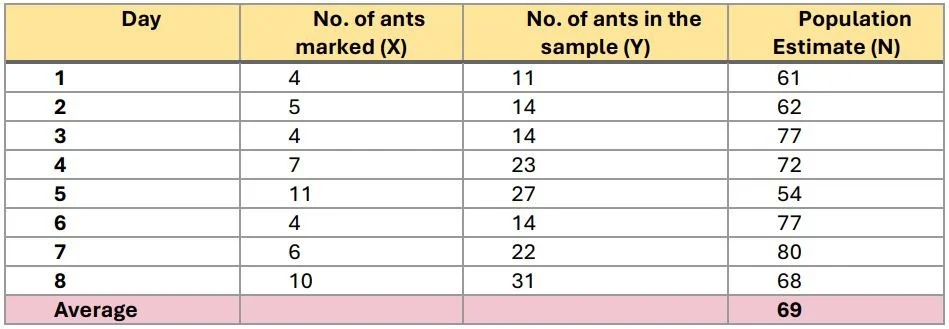
2. In an unknown population number (N), we marked 22 animals (Z)
3. On the first day, we counted (and recorded) a sample of 11 ants (Y).
4. Of the 11, 4 were marked (X). Remember, the proportion of those marked animals in the sample is equivalent to the proportion of the number of animals you marked in the whole population. Or, X/Y = Z/N.
5. Substituting for our number of marked ants, 4/11 = 22/N
6. Solving for N,
22/N = 4/11
N = 22 x 11/4
= 60.5 (61)
7. Below are some real numbers from our trial.
Activity
Students in the Classroom:
METHOD
1. As students come into the room, hand out randomly 10 pieces of paper.
2. Allow students to sit randomly throughout the classroom, and not together.
3. When all are seated, choose 10 students at random and ask them to stand if they have a piece of paper.
4. Count them.
5. For example, 4 out of the 10 have a piece of paper.
6. The ‘population size’ is calculated as 10/4 x 10 = 25.
Activity
Marbles in a Bottle
We can estimate the size of a population using the example of marbles in a bottle.
1. Start with 100 black marbles in our bottle – the population size is thus 100.
2. Replace 20 of the black marbles with 20 white ones – this is equivalent to ‘marking’ our animals.
3. Replace the white marbles in the bottle and mix all marbles well.
4. Remove 10 marbles randomly from the bottle and count how many of them are white.
As an example, 2 out of the 10 are white.
• We know that there is a total of 20 white marbles in the bottle.
• If 2 are marked in our sample of 10, then there should be 10/2 x 20 marbles in the bottle, or 100.
There is a big element of chance in the estimation.
• if we had found 3 white marbles in our sample of 10, we would then estimate the population size to be 10/3 x 20 which equals 66.7, and not 100.
Our estimate of the population size works best when many animals in the population are marked, and when we take a large sample size.
• In the example above, if 50% of them had been white and our sample size was 20 instead of 10, we would have a better estimate of the total marble population.