On Country

Measure The Height of a Tree

This activity suits tall trees. Originally, it was used for timber producers to estimate the merchantable timber in a tree’s trunk.

Background

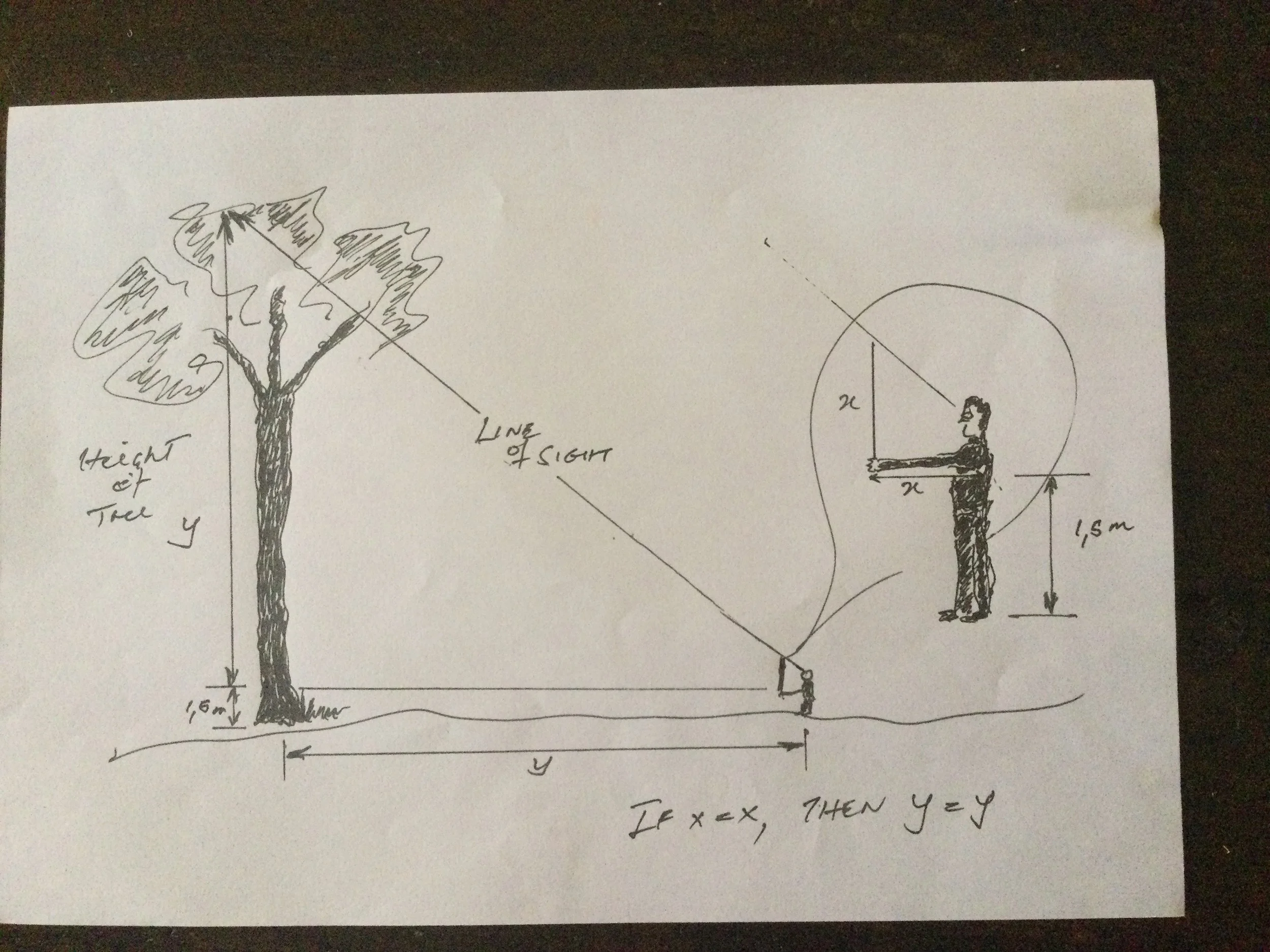
From the diagram, • the distance between the end of the stick to the eye is the same, whether the stick is held along the arm or upright in the hand. • in other words the 2 sides of the right-angled triangle are the same, X=X. • Maintaining the right-angle, the triangle is enlarged, but still with 2 equal sides (Y=Y). • Therefore, distance along the ground is the same as the height of the tree.

Activity

Measure the Height of a Tall Tree:

MATERIALS

• a tree with a measurable trunk – eg. an upright tree such as a Wandoo, or another tall eucalypt.

• a stick the same length as the student’s hand to eye or hand to shoulder (effectively, the length of the student’s arm).

• tape measuring to 10m.

Teacher Note: If a 10m tape is not available, mark the spot where the student is standing (when focussing the end of the stick at the top of the tree), and have them pace out the distance to the tree trunk. Record. In the classroom, the student measures the length of the pace and calculates the total distance.

METHOD

1. Locate a tall tree.

2. Hold the stick in the hand and check that its length is equal to the distance between the eye (or shoulder) and the hand – Distance X (see diagram).

3. Hold the stick upright at the end of your arm to form a right angle of 90o (see diagram). You will notice that you have made a right-angled isosceles triangle with 2 equal sides - Length of X. The hypotenuse of the triangle is the distance between your eye and the top of the stick.

4. Maintaining the same right angle of 90o, walk backward away from the tree on level ground, sighting across the upper end of the stick you are holding upright, until it rests at the top of the tree.

5. You will notice that you have simply enlarged the right-angled isosceles triangle by extending one of the sides, the distance Y that you walked from the base of the tree. By definition, the other side of the isosceles triangle (the height of the tree) is the same distance, Y.

6. A small correction should be made to account for the height of the extended arm from the ground. Measure the student‘s height to their shoulder and add to the length Y.

Adapted from Education Resources Information Center. https://eric.ed.gov

Measuring height of a tree. Sketch: Don Bradshaw.