MODULE 2
Angles
Measure The Height of a Tree
This activity suits tall trees. Originally, it was used for timber producers to estimate the merchantable timber in a tree’s trunk.
Background
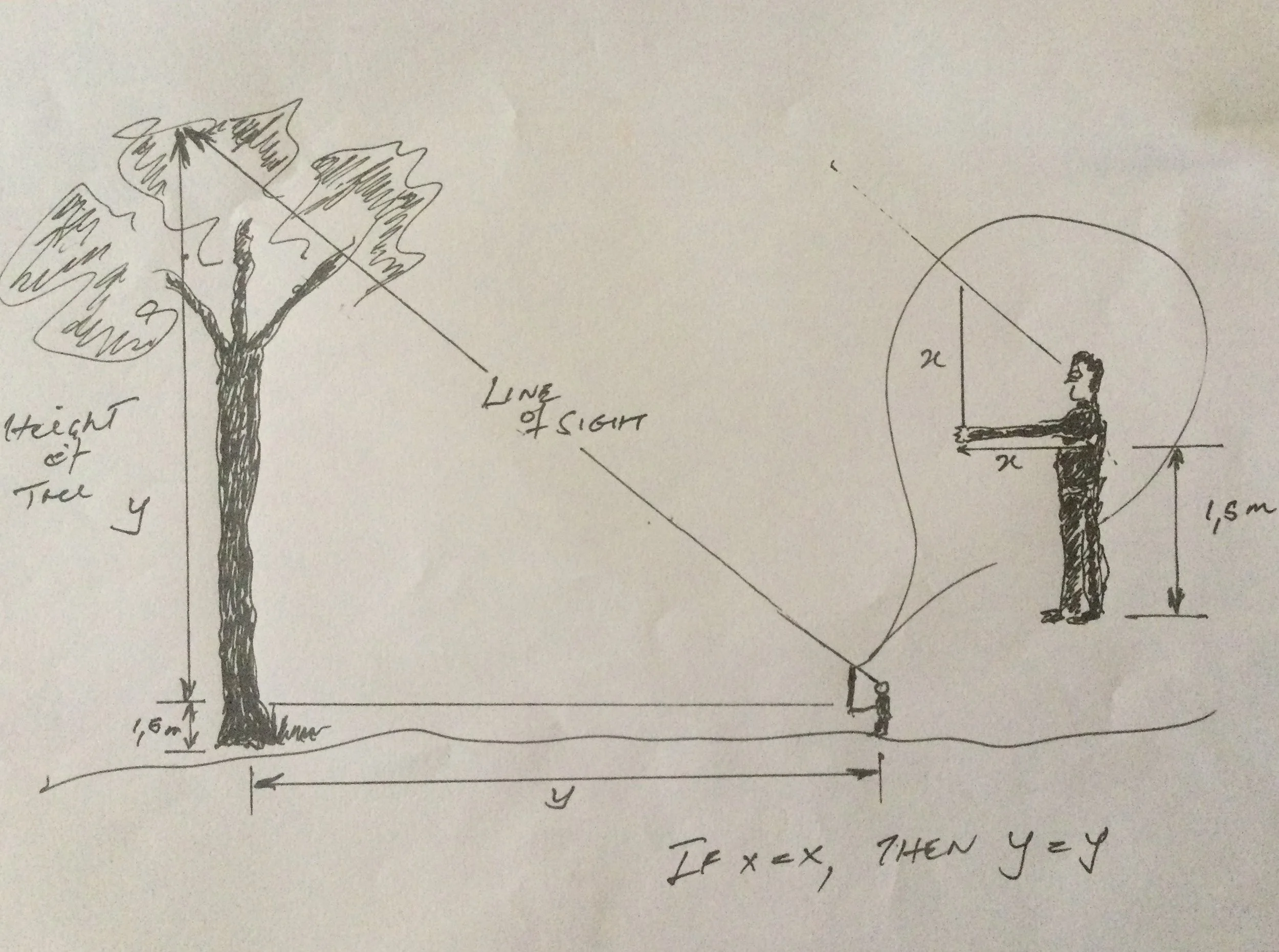
From the diagram,
• the distance between the end of the stick to the eye is the same, whether the stick is held along the arm or upright in the hand.
• in other words the 2 sides of the right-angled triangle are the same, X=X.
• Maintaining the right-angle, the triangle is enlarged, but still with 2 equal sides (Y=Y).
• Therefore, distance along the ground is the same as the height of the tree.
Red Morrel.
Activity
Measure the Height of a Tall Tree:
MATERIALS
• a tree with a measurable trunk – eg. an upright tree such as a Wandoo, or another tall eucalypt.
• a stick the same length as the student’s hand to eye or hand to shoulder (effectively, the length of the student’s arm).
• tape measuring to 10m.
Teacher Note: If a 10m tape is not available, mark the spot where the student is standing (when focussing the end of the stick at the top of the tree), and have them pace out the distance to the tree trunk. Record. In the classroom, the student measures the length of the pace and calculates the total distance.
METHOD
1. Locate a tall tree.
2. Hold the stick in the hand and check that its length is equal to the distance between the eye (or shoulder) and the hand – Distance X (see diagram).
3. Hold the stick upright at the end of your arm to form a right angle of 90o (see diagram). You will notice that you have made a right-angled isosceles triangle with 2 equal sides - Length of X. The hypotenuse of the triangle is the distance between your eye and the top of the stick.
4. Maintaining the same right angle of 90o, walk backward away from the tree on level ground, sighting across the upper end of the stick you are holding upright, until it rests at the top of the tree.
5. You will notice that you have simply enlarged the right-angled isosceles triangle by extending one of the sides, the distance Y that you walked from the base of the tree. By definition, the other side of the isosceles triangle (the height of the tree) is the same distance, Y.
6. A small correction should be made to account for the height of the extended arm from the ground. Measure the student‘s height to their shoulder and add to the length Y.
Adapted from Education Resources Information Center. https://eric.ed.gov
Measuring height of a tree. Sketch: Don Bradshaw.
Distance of a Projectile
An Introduction to Vectors
Definitions
A vector is an object with magnitude and direction (velocity, force, acceleration, etc). A scalar is an object with just magnitude (temperature, pressure, age, length). A vector, denoted ➔v or v, has no initial point and is often best thought of as at the origin.
http://web.eecs.umich.edu/~sugih/courses/eecs487/common/notes/VM.pdf
Vector projection
The vector projection of 1 vector over another vector is the length of the shadow of the given vector over another vector. It is obtained by multiplying the magnitude of the given vectors with the cosecant of the angle between the two vectors. The resultant of a vector projection formula is a scalar value.
https://www.cuemath.com/geometry/projection-vector/
Projection vector formula
The projection of vector a➔ (in the diagram) on vector b➔ is equal to the product of vector a and b, divided by the magnitude (length) of vector b, giving a scalar value, (a x b)/b.
Activity
Measure the Distance Travelled of a Projectile Launched from Different Angles at a Constant Force:
MATERIALS
1. Using a marble launcher (See Equipment in TOOLBOX)
• marble launcher
• marbles
• measuring tape
• notebook & pencil
2. Using a foam javelin (See Equipment in TOOLBOX)
• foam javelin
• protractor
• measuring tape
• notebook & pencil
METHOD
1. Students predict at which angle the marble (or javelin) will travel the furthermost.
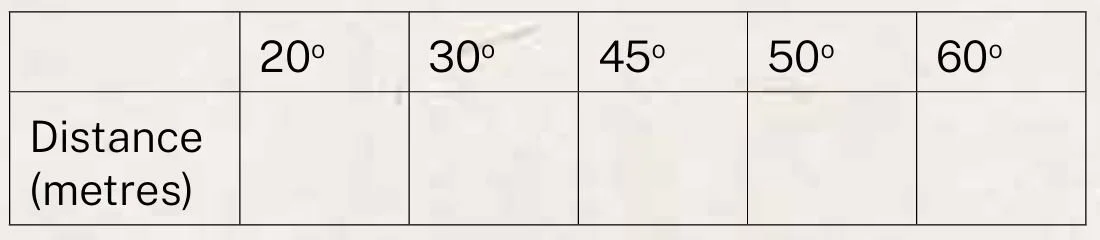
2. Using the launcher (which should project with a constant force), each student projects a marble at angles of 20o, 45o, and 60o (or others in addition).
3. Measure the distance travelled by the marble each time, and record.
4. Average the results at each angle and enter a Class Table.
5. Using the javelin, have the student launcher project the javelin at different angles (keeping the force constant).
6. Using a protractor, measure the angle at each throw made by the student’s body and the straight arm at launching.
7. Measure the distance travelled by the javelin each time, and record.
8. Average the results at each angle and enter a Class Table.
9. RECORD results in a Table, labelled with the method chosen.
• Draw a diagram similar to that shown in the Figure, measuring the angle and distance along the x-axis, with each angle measured.
• Develop a scale that associates an angle with a distance.
Angle of projection. From Cuemath
Marble launcher
Angle of a Projectile From an Antlion’s Pit
Angle of a Projectile from an antlion’s pit
Reference:
http://www.antlionpit.com/antlions.html
Follow the prompts to the antlion behaviour and life cycle.
• The antlion (the larva of the Lace-wing fly) digs a pit in loose dry sandy soil with a spiral action, throwing the sand up and outwards with its head. It appears to be selecting the size of the sand grains, as it throws the larger ones out, retaining the finer ones.
• In addition, it engineers the angle of the side of the pit to 30o. This ensures the fine particles (which will have less momentum) stay on sloping walls, while larger particles (which will have greater momentum) tend to fall to the centre, the fate of a future prey.
• It is thus the size of the sand grain and the angle of the sides of the pit that ensure an ant will be carried into the waiting jaws, just visible at the bottom of the pit.
• The antlion clamps them around the prey, injects a toxin and proceeds to suck the soft inner parts of the ant.
• When finished, it tosses the exoskeleton of the ant out of the pit – at an angle of 45o.
• This is the angle (well known to javelin throwers), that will maximise the distance travelled of a thrown (or projected) object.
Activity
Using the scale (angle/ distance), predict what might happen to the prey remains if the antlion alters its angle of throw (presuming it uses the same force with each throw):
1. Draw the pit, indicating where the prey remains will land at each angle.
2. Predict the length of the radius of the pit that will maximise the prey remains landing outside the pit.
Antlion trap
Antlion
Glossary
aridity – lack of water
cells – basic building blocks of all things
condensation – the reclaiming of water molecules from water vapour
desiccation – drying out
diffusion - the process resulting from random motion of molecules resulting in a net flow of matter from a region of high concentration to a region of low concentration.
equilibrium – a state where opposite forces are balanced so one isn’t stronger than the other
evaporation – the net loss of water molecules from the surface of a liquid(7)
1. Noble, J. C., Kimber, R. G., On the ethno ecology of mallee root-water. Aboriginal History 21, 170-202 (1997).
2. Bradshaw, S. D., Vertebrate Ecophysiology:an Introduction to its principles and applications. Cambridge University Press, (2003), pp. 287.
3. Bentley, P. J., Blumer, W. F. C., Uptake of Water by the Lizard, Moloch horridus. Nature (London) 194, 699-700 (1962).
4. Cartledge, V. A., Withers, P. C., Bradshaw, S. D., Water balance and Arginine Vasotocin in the Cocooning frog Cyclorana platycephala (Hylidae). Physiological and Biochemical Zoology 81, 43-53 (2008).
isotonic - When the concentration of a solvent (i.e water containing solutes) is the same inside as outside the membrane – a thin, soft layer of material that separates two things
osmosis – the diffusion of molecules through a membrane, from a high concentration to a lower concentration.
semi-permeable – only certain, small molecules can pass through
solute – a substance that dissolves (like sugar in water)
solvent – a substance that is able to dissolve other substances (like the water that dissolves the sugar) cell
xerophyte - any plant adapted to life in a dry or physiologically dry habitat (salt marsh, saline soil, or acid bog) by means of mechanisms to prevent water loss or to store available water.
Reference
5. Crews, D., Sex determination: where environment and genetics meet. Evolution and Development 5, 50-55 (2003).
6. Nowack, J., Cooper, C. E., Geiser, F., Cool echidnas survive the fire. Proceedings of the Royal Society B 283, (2016).
7. Feynman, R. P., Ed., Six Easy Pieces; Essentials of Physics explained by its most brilliant teacher, Basic Books, New York, (2011).